Understanding Alternating Current (AC) : Part 2
Continued from Alternating Current - Part 1...
Frequency
The number of cycles of AC per second is referred to as the Frequency, and is measured in Hertz. Most AC equipment are rated by frequency as well as by voltage and current.
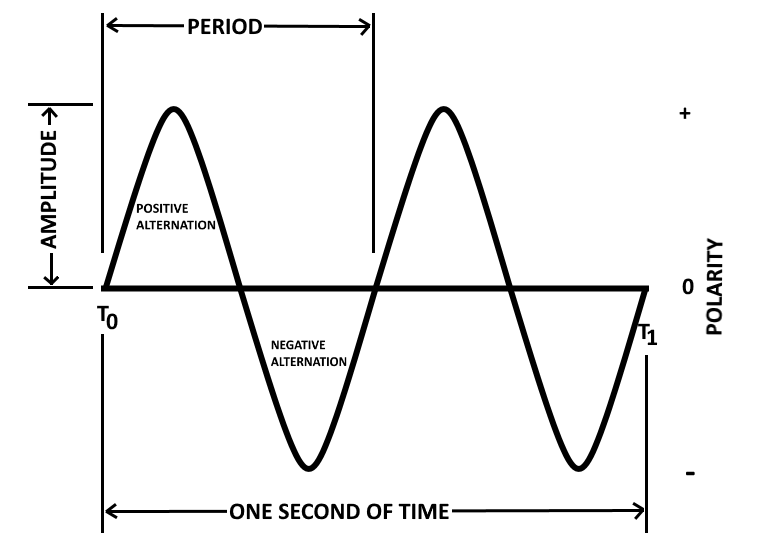
A cycle consists of two complete alternations in a period of time. The term HERTZ (Hz) has been designated to indicate one cycle per second. If one cycle per second is one hertz, then 100 cycles per second are equal to 100 hertz, and so on.
In the previous example above, if the loop makes one complete revolution each second, the generator produces one complete cycle of AC during each second (1 Hz). Increasing the number of revolutions to two per second will produce two complete cycles of AC per second (2 Hz). The number of complete cycles of alternating current or voltage completed each second is referred to as the Frequency. Frequency is always measured and expressed in hertz.
Alternating-current frequency is an important term to understand since most AC electrical equipment requires a specific frequency for proper operation.
Period
An individual cycle of any sine wave represents a definite amount of Time. If we have a sine wave which shows 2 cycles that has a frequency of 2 hertz (Hz), since 2 cycles occur each second, 1 cycle must require one-half second of time. The time required to complete one cycle of a waveform is called the Period Of The Wave.
The relationship between time (t) and frequency (f) is indicated by the formula :
| t = 1/f and f = 1/t | where t= period in seconds, and f = frequency in hertz |
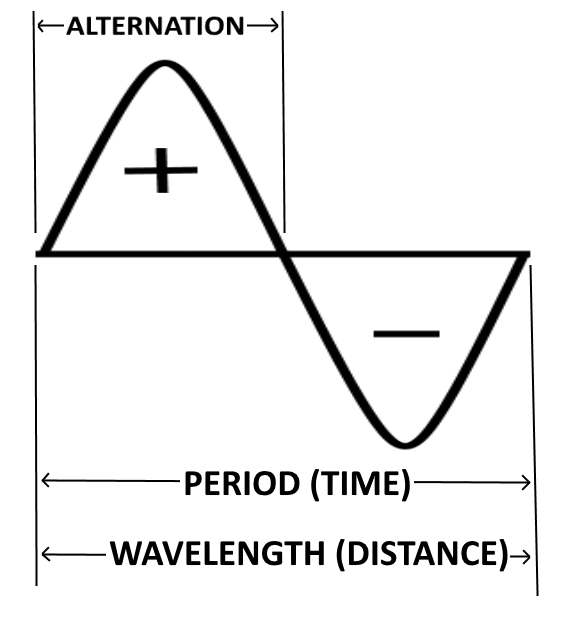
Each cycle of the sine wave shown so far consists of one or more identically shaped variations in voltage. The variation which occurs during the time the voltage is positive is called the Positive Alternation. The variation which occurs during the time the voltage is negative is called the Negative Alternation. In a sine wave, these two alternations are identical in size and shape, but opposite in polarity.
| AC Sine Wave at 2Hz |
The distance from zero to the maximum value of each alternation is called the Amplitude. The amplitude of the positive alternation and the amplitude of the negative alternation are the same.
Wavelength
The time it takes for a sine wave to complete one cycle is defined as the Period of the waveform. The distance traveled by the sine wave during this period is referred to as Wavelength. Wavelength, indicated by the symbol λ (Greek lambda), is the distance along the waveform from one point to the same point on the next cycle. The point on the waveform that measurement of wavelength begins is not important as long as the distance is measured to the same point on the next cycle.
| Wavelength |
Alternating Current Values
In discussing alternating current and alternating voltage, you will often find it necessary to express the current and voltage in terms of Maximum or Peak values, Peak-To-Peak values, Effective values, Average values, or Instantaneous values. Each of these values has a different meaning and is used to describe a different amount of current or voltage.
- Peak and Peak-To-Peak Values : The maximum value reached during one alternation of a sine wave is the peak value. The maximum reached during the positive alternation to the maximum value reached during the negative alternation is the peak-to-peak value. The peak-to-peak value is twice the peak value.
- Effective Values : The value of alternating current or voltage that produces the same amount of heat in a resistive component that would be produced in the same component by a direct current or voltage of the same value. The effective value of a sine wave is equal to 0.707 times the peak value. The effective value is also called the root mean square or rms value. The term rms value is used to describe the process of determining the effective value of a sine wave by using the instantaneous value of voltage or current. You can find the rms value of a current or voltage by taking equally spaced instantaneous values on the sine wave and extracting the square root of the average of the sum of the instantaneous values. The formulas for effective and maximum values of voltage and current are:
Eeff = 0.707 * Emax Emax = 1.414 * Eeff Ieff = 0.707 * Imax Imax = 1.414 * Ieff - Average Values : The average value of a sine wave of voltage or current is the average of all the instantaneous values during one alternation. The average value is equal to 0.636 of the peak value. The formulas for average voltage and average current are:
Eavg = 0.636 * Emax Iavg = 0.636 * Imax - Instantaneous Values : Is the value of voltage or current at one particular instant of time. There are an infinite number of instantaneous values between zero and the peak value.
Ohm's Law In AC Circuits
Many AC circuits contain resistance only. The rules for these circuits are the same rules that apply to DC circuits. Resistors, lamps, and heating elements are examples of resistive elements. When an AC circuit contains only resistance, Ohm's Law, Kirchoff's La, and the various rules that apply to voltage, current, and power in a DC circuit also apply to the AC circuit.
The Ohm's Law formula for an AC circuit can be stated as:
| Ieff = Eeff / R |
| or |
| I = E / R |
Remember, unless otherwise stated, all AC voltage and current values are given as effective values. The formula for Ohm's Law can also be stated as:
| Iavg = Eavg / R or Imax = Emax / R |
| Or |
| Ipeak-to-peak = Epeak-to-peak / R |
The important thing to keep in mind is: Do Not Mix AC Values. When you solve for effective values, all values you use in the formula must be effective values. Similarly, when you solve for average values, all values you use must be average values.
Phase
When a sine wave of voltage is applied to a resistance, the resulting current is also a sine wave. This follows Ohm's law which states that current is directly proportional to the applied voltage. The sine wave of voltage and the resulting sine wave of current are superimposed on the same time axis. As the voltage increases in a positive direction, the current increases along with it, and then when the voltage reverses direction, the current also reverses direction. When two sine waves are precisely in step with one another then they are said to be In Phase. To be in phase, the two sine waves must go through their maximum and minimum points at the same time and in the same direction.
In some circuits, several sine waves can be in phase with each other. Thus, it is possible to have two or more voltage drops in phase with each other and also be in phase with the circuit current.
If the voltage waves of two sine waves do not go through their maximum and minimum points at the same instant of time, a Phase Difference exists between the two waves, and therefore the two waves are said to be Out Of Phase.
To further describe the phase relationship between two sine waves, the terms Lead and Lag are used. The amount by which one sine wave leads or lags another sine wave is measured in degrees. It is the phase relationship between the two sine waves that is important.
It is possible for one sine wave to lead or lag another sine wave by any number of degrees, except 0° and 360°. When the latter condition exists, the two waves are said to be in phase. Thus, two sine waves that differ in phase by 45° are actually out of phase with each other, whereas two sine waves that differ in phase by 360° are considered to be in phase with each other.
A very common phase relationship that is often seen in some circuits is when two waves differ in phase by exactly 180°. In this condition, even though the waves pass through their maximum and minimum values at the same time, their instantaneous voltages are always of opposite polarity. If two such waves exist across the same component, and the waves are of equal amplitude, they cancel each other. When they have different amplitudes, the resultant wave has the same polarity as the larger wave and has an amplitude equal to the difference between the amplitudes of the two waves (another words, they almost cancel each other out, but since they don't fully cancel each other out then the remaining voltage and current left over still remains present).
To determine the phase difference between two sine waves, locate the points on the time axis where the two waves cross the time axis traveling in the same direction. The number of degrees between the crossing points is the phase difference. The wave that crosses the axis at the later time (to the right on the time axis) is said to lag the other wave.
Final Thoughts
Thank you for reading, I hope you found this blog post educational and helpful in some way.